
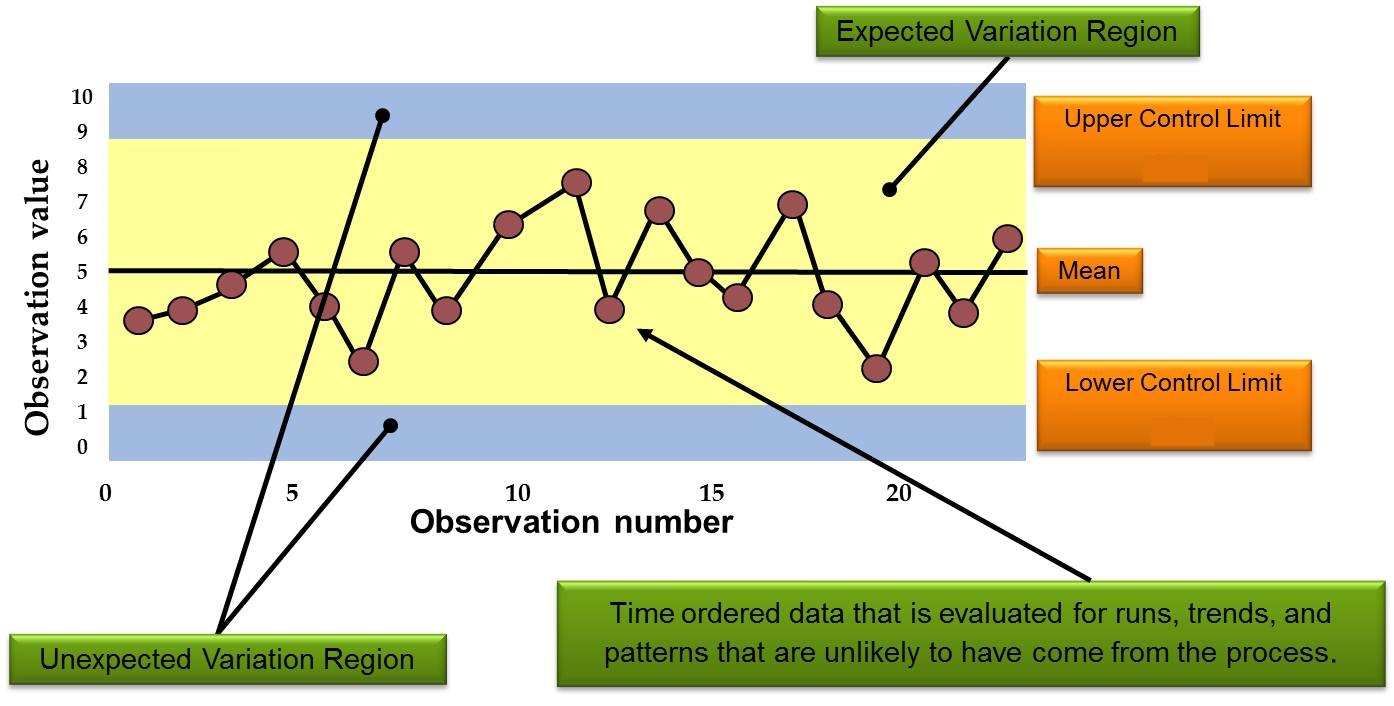
But the basic difference is that, unlike the X bar chart, they consider the previous value means at each point. The cumulative sum ( CUSUM) and the exponentially weighted moving average ( EWMA) charts also monitor the mean of the process. Additionally, it is an example of statistical process control. These combination charts help to understand the stability of processes and detect the presence of special cause variation. It is actually two plots to monitor the process mean and the process range (as described by standard deviation) over time. With a large sample size in the subgroup, the standard deviation is a better measure of variation than the range because it considers all the data, not just minimum and maximum values. Manually, it is very easy to compute the X Bar R Control chart, whereas the sigma chart may be difficult due to tedious calculations and large sample sizes. Selection of an appropriate control chart is very important in control chart mapping, otherwise ended up with inaccurate control limits for the data. The basic difference is that X bar S charts plot the subgroup standard deviation, whereas R charts plot the subgroup range. X bar S charts are also similar to X Bar R Control charts. Conversely, the S charts provide a better understanding of the spread of subgroup data than the range. These charts are used when the subgroups have large sample sizes. X Bar S charts often use control charts to examine the process mean and standard deviation over time.


 0 kommentar(er)
0 kommentar(er)
